







Os Sólidos de Arquimedes
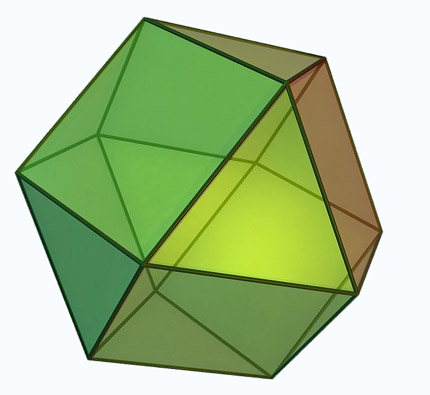
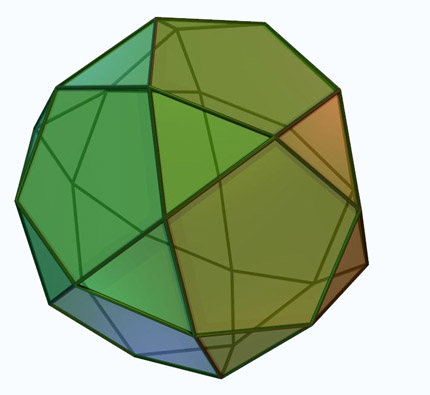
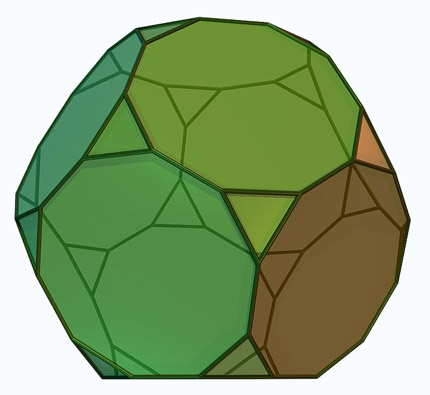
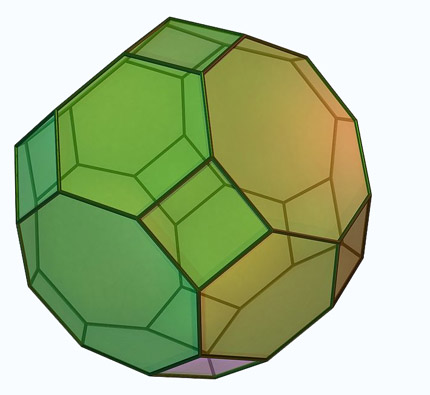
Sólidos de Arquimedes ou poliedros semi-regulares são poliedros convexos cujas faces são polígonos regulares de mais de um tipo. Todos os seus vértices são congruentes, isto é, existe o mesmo arranjo de polígonos em torno de cada vértice. Além disso, todo vértice pode ser transformado em outro vértice por uma simetria do poliedro.
Existem apenas treze poliedros arquimedianos.
Onze são obtidos truncando sólidos platónicos:O Tetraedro truncado, o Cuboctaedro, o Cubo truncado, o Octaedro truncado, o Rombicuboctaedro, o Cuboctaedro truncado, o Icosidodecaedro, o Dodecaedro truncado, o Icosaedro truncado, o Rombicosidodecaedro e o Icosidodecaedro truncado.
Dois que são obtidos por snubificação de sólidos platónicos:O Cubo snub e o Icosidodecaedro snub. Estes dois sólidos têm caso isomórfico, quer dizer uma figura de espelho correspondente.Os sólidos duais dos sólidos de Arquimedes são os Sólidos de Catalan.
in Wikipédia
LRO
LRO




